repunit
(another Prime Pages' Glossary entries)
The Prime Glossary
Glossary: Prime Pages: Top 5000: The term repunit comes from the words 'repeated' and 'unit;' so repunits are positive integers in which every digit is one. (This term was coined by A. H. Beiler in [Beiler1964].) For example, R1=1, R2=11, R3=111, and Rn=(10n-1)/9. Notice Rn divides Rm whenever n divides m.

Repunit primes are repunits that are prime. For example, 11, 1111111111111111111, and 11111111111111111111111 (2, 19, and 23 digits). The only other known repunit primes are the ones with 317 digits: (10317-1)/9; and with 1,031 digits: (101031-1)/9.

During 1999 Dubner discovered R49081 = (1049081-1)/9 was a probable prime, and in October 2000, Lew Baxter discovered the next repunit probable prime after that is R86453. In 2007 the probable primes R109297 (Bourdelais and Dubner) and R270343 (Voznyy and Budnyy) were found. It will be some time before these giants is proven prime! As the poet wrote:

Ah, but a mans reach should exceed his grasp, or whats a heaven for? (Robert Browning)
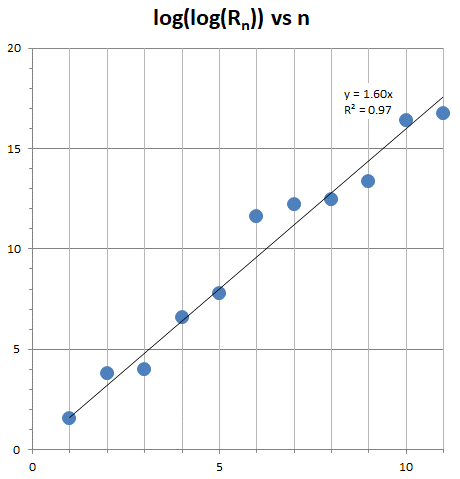
Even though only a few are known, it has been conjectured that there are infinitely many repunit primes. To see why just look at the graph of the known repunit primes and probable primes (here we graph log(log(Rn)) verses n.
Graph

Because of their very special form, a repunit prime is also a circular prime and a palindromic prime.

See Also: GeneralizedRepunit

References:

Beiler1964
A. Beiler, Recreations in the theory of numbers, Dover Pub., New York, NY, 1964.
BLSTW88
J. Brillhart, D. H. Lehmer, J. L. Selfridge, B. Tuckerman and S. S. Wagstaff, Jr., Factorizations of bn ± 1, b=2,3,5,6,7,10,12 up to high powers, Amer. Math. Soc., Providence RI, 1988.  pp. xcvi+236, ISBN 0-8218-5078-4. MR 90d:11009 (Annotation available)
Dubner2002
Dubner, Harvey, "Repunit R49081 is a probable prime," Math. Comp., 71:238 (2002) 833--835 (electronic).  (http://dx.doi.org/10.1090/S0025-5718-01-01319-9) MR 1885632 (Abstract available)
WD86
H. C. Williams and H. Dubner, "The primality of R1031," Math. Comp., 47:176 (1986) 703--711.  MR 87k:11141
Yates82
S. Yates, Repunits and repetends, Star Publishing Co., Inc., Boynton Beach, Florida, 1982.  pp. vi+215, MR 83k:10014


Chris K. Caldwell © 1999-2013 (all rights reserved)