|
floor function (another Prime Pages' Glossary entries) |
|
|
Glossary:
Prime Pages:
Top 5000:
|
The floor function of x, historically called the greatest integer function, is the greatest integer less than or equal to x. This function is sometimes written [x], but is best written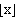  (a notation that was suggested by Iverson in 1962) to differentiate it from the ceiling function.
Examples: [3.14159]=3, [-3.14159]=-4, and [log(n)/log(10)]+1 is the number of digits in the decimal expansion of the positive integer n.
See Also: CeilingFunction References:
Chris K. Caldwell © 1999-2013 (all rights reserved)
|