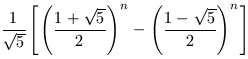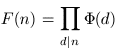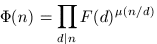|
primitive part (another Prime Pages' Glossary entries) |
|
|
Glossary:
Prime Pages:
Top 5000:
|
Many sequences have the useful divisibility property that F(n) divides F(mn) for positive integers m and n. Examples of such sequences include the Fibonacci numbers, the Lucas sequences and polynomial sequences such as xn-1 and c(xn-yn). In fact this last example includes the others because the Fibonacci numbers may be written: and the Lucas sequences have similar definitions. When this divisibilty property holds we may define the
primitive part (or primitive factor) so that Here  is the Möbius function (and the equations
above are a special case of the product form of the Möbius
inversion formula
[Apostol76 Chpt 2]).
Often, but not always, the primitive part of such an F(n) is the maximal divisor of F(n) which is coprime to F(d) for all divisors d of n. When factoring such sequences, we always first divide them into their primitive parts, and on occassion we are lucky and the primitive parts are prime. The prime pages' Top Twenty collection has several pages dedicated to such primitive divisors. Other sequences with similar divisibility properties also have primitive parts. When defining the primitive parts, additional divisors may be removed from the terms (as in the Lehmer primitive parts) or Aurifeuillian factorizations may need to be acknowledged (as in the Lucas Aurifeuillian primitive parts).
Related pages (outside of this work)
References:
Chris Caldwell © 1999-2009 (all rights reserved)
|
(n) of F(n) as follows:
