unique prime
The reciprocal of every prime p (other than two and five) has a period, that is the decimal expansion of 1/p repeats in blocks of some set length (see the period of a decimal expansion). This is called the period of the prime p. Samuel Yates defined a unique prime (or unique period prime) to be a prime which has a period that it shares with no other prime. For example: 3, 11, 37, and 101 are the only primes with periods one, two, three, and four respectively--so they are unique primes. But 41 and 271 both have period five, 7 and 13 both have period six, 239 and 4649 both have period seven, and each of 353, 449, 641, 1409, and 69857 have period thirty-two, showing that these primes are not unique primes.As we would expect from any object labeled "unique," unique primes are extremely rare. For example, even though there are over 1047 primes below 1050, only eighteen of these primes are unique primes (all listed in the table below). We can find the unique primes using the following theorem.
- Theorem.
- The prime p is a unique prime of period n
if and only if
is a power of p where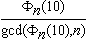
.gif) is the nth cyclotomic polynomial.
is the nth cyclotomic polynomial.
It is possible to generalize this to other bases, and
the generalized unique primes in base-x (any integer greater than one) are the prime factors of ![]() which do not divide x.
which do not divide x.
| period | prime |
|---|---|
| 1 | 3 |
| 2 | 11 |
| 3 | 37 |
| 4 | 101 |
| 10 | 9091 |
| 12 | 9901 |
| 9 | 333667 |
| 14 | 909091 |
| 24 | 99990001 |
| 36 | 9999990000 01 |
| 48 | 9999999900 000001 |
| 38 | 9090909090 90909091 |
| 19 | 1111111111 111111111 |
| 23 | 1111111111 1111111111 111 |
| 39 | 9009009009 0099099099 0991 |
| 62 | 9090909090 9090909090 9090909091 |
| 120 | 1000099999 9989998999 9000000010 001 |
| 150 | 1000009999 9999989999 8999990000 0000010000 1 |
Related pages (outside of this work)
- The largest known unique primes
- The largest known generalized unique primes
References:
- Caldwell97
- C. Caldwell, "Unique (period) primes and the factorization of cyclotomic polynomial minus one," Mathematica Japonica, 46:1 (1997) 189--195. MR 99b:11139 (Abstract available)
- CD1998
- C. Caldwell and H. Dubner, "Unique period primes," J. Recreational Math., 29:1 (1998) 43--48.
- Yates1980
- S. Yates, "Periods of unique primes," Math. Mag., 53:5 (1980) 314.
Printed from the PrimePages <t5k.org> © Reginald McLean.