Here we address the following frequently asked question.
Is there a formula for producing a specific prime number? Let
me give you an example. The formula is given the number 52. In return,
the formula produces 239, the fifty-second prime number (I think).
Yes, there are many such formulas--but they are of recreational use only
because they are very inefficient. Most are either ways of encoding the
list of primes or very clever counting arguments. I will give a couple example
below, but for more information start with chapter three "Are There Functions
Defining Prime Numbers?" of Ribenboim's text [Ribenboim95
pp. 179-212].
Method One: Encoding Primes
Let pn be the nth prime. In 1952 Sierpinski
suggested we define a constant A as follows:
A = = 0.02030005000000070...
Then using the floor function [x] (the greatest integer less than
or equal to x) we have
pn =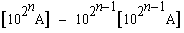
Hardy and Wright [HW79
p345] give a variant of this: Let r be an integer greater than one
and define a constant B as follows:
B =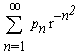
then
pn =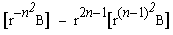
This type formula would only be of value if the necessary constant could
be found without first finding the primes--this may be possible,
but it seems unlikely.
Method Two: Counting Primes with Wilson's Theorem
First use one of these three methods to define pi(x). Willans (1964) used
pi(n) = (sum from j=2 to n) sin2(pi*(j-1)!2/j)
/ sin2(pi/j).
Minác (unpublished, proof in [Ribenboim95,
p181]) set
pi(n) = (sum from j=2 to n) [ ((j-1)!
+ 1)/j - [(j-1)!/j] ].
Hardy and Wright set pi(1) = 0, pi(2) = 1, and then [HW79
p414]
pi(n) = 1 + (sum from j=3 to n) ( (j-2)!
- j[(j-2)!/j] ).
(for all n>2). Then we have (still using the floor function [x]):
nth prime = 1 + (sum from m=1 to j=2n)
[ [ n/(1 + pi(m)) ]1/n ]
= 0.02030005000000070... 
