Goldbach's Proof of the Infinitude of Primes (1730) 
(From the Prime Pages' list of proofs)


Home
Search Site

Largest
The 5000
Top 20
Finding
How Many?
Mersenne

Glossary
Prime Curios!
Prime Lists

FAQ
e-mail list
Titans

Prime Links
Submit primes

Euclid may have been the first to give a proof that there are infintely many primes, but his proof has been followed by many others.  Below we give Goldbach's clever proof using the Fermat numbers (written in a letter to Euler, July 1730), plus a few variations.  See the page "There are Infintely Many Primes" for several more proofs.

First we need a lemma.

Lemma.
The Fermat numbers Fn = 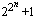2^2^n+1 are pairwise relatively prime.

Proof.
It is easy to show by induction that Fm-2 = F0.F1.....Fm-1.  This means that if d divides both Fn and Fm (with n < m), then d also divides Fm-2; so d divides 2.  But every Fermat number is odd, so d is one.
Now we can prove the theorem:
Theorem.
There are infinitely many primes.

Proof.
Choose a prime divisor pn of each Fermat number Fn.  By the lemma we know these primes are all distinct, showing there are infinitly many primes.

Note that any sequence that is pairwise relatively prime will work in this proof.  This type of sequence is easy to construct.  For example, choose relatively prime integers a and b, then define an as follows.

a1=a,
a2=a1+b,
a3=a1a2+b,
a4=a1a2a3+b,
...
This includes both the Fermat numbers (with a=1,b=2) and Sylvester's sequence (with a=1,b=2):
a1=2 and an+1= an2-an+1.
In fact, the proof really only needs a sequence which has a subsequence which is pairwise relatively prime, e.g., the Mersenne numbers.
The Prime Pages
Another prime page by Chris K. Caldwell <caldwell@utm.edu>