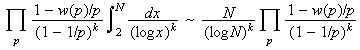Dickson's conjecture
Dickson conjectured in 1904 that given a family of linear functions with integer coefficients ai > 1 and bi:
a1n + b1, a2n + b2, akn + bk,
then there are infinitely many integers n > 0 for which these are simultaneously prime unless they "obviously cannot be" (that is, unless there is a prime p which divides the product of these for all n). This is now called Dickson's Conjecture.
Many conjectures follow from Dickson's conjecture. For example, if the functions are n and n+2, then Dickson's conjecture implies the twin prime conjecture. If the functions are n and 2n+1, then we have the conjecture that there are infinitely many Sophie Germain primes. The prime k-tuple conjecture is also a special case of Dickson's conjecture, as is the conjecture that for each positive integer n, there is an arithmetic sequence of n primes. Finally, if Dickson's conjecture is true, then there are infinitely many composites Mersenne numbers as well as infinitely many Carmichael numbers with just three prime factors.
Schinzel and Sierpinski extended Dickson's conjecture into the analogous Hypothesis H for integer polynomials with arbitrary degree.
Dickson's conjecture can be heuristically quantified as follows. Let w(p) be the number of solutions to
(a1n + b1)(a2n + b2).....( akn + bk) = 0 (mod p).
Then the expected number of positive integers n less than N which yield k simultaneous primes
a1n + b1, a2n + b2, akn + bk,
is conjectured to be asymptotic to
where the products are taken over the set of all primes p.
If we replace "there are infinitely many integers n > 0 for which these are simultaneously prime" in Dickson's conjecture with "there is an integer n > 0 for which these are simultaneously prime," then we appear to weaken the conjecture. But it is easy to show these two conjectures are equivalent!
Another important conjecture that follows from Dickson's conjecture is that if a1 < a2 < ... < ak are nonzero integers for which there is no prime dividing the product
(x + a1)(x + a2).....(x + ak)
for all integers n, then there are infinitely many positive integers n for which
x+a1, x+a2, . . . x+ak,
are consecutive primes.
This form of Dickson's conjecture implies that for each positive integer n, there are infinitely many arithmetic sequence of n consecutive primes. It also implies Polignac's conjecture, and ...
Related pages (outside of this work)
References:
- Ribenboim95 (chapter 6)
- P. Ribenboim, The new book of prime number records, 3rd edition, Springer-Verlag, New York, NY, 1995. pp. xxiv+541, ISBN 0-387-94457-5. MR 96k:11112 [An excellent resource for those with some college mathematics. Basically a Guinness Book of World Records for primes with much of the relevant mathematics. The extensive bibliography is seventy-five pages.]
- SS58
- A. Schinzel and W. Sierpinski, "Sur certaines hypotheses concernment les nombres premiers," Acta. Arith., 4 (1958) 185-208. Erratum 5 (1958).