least common multiple
The least common multiple of two (or more) nonzero integers is the least positive integer divisible by all of them. This is usually denoted lcm. For example, lcm(-12,30)=60. Notice
- gcd(a,b).lcm(a,b) = ab, and
- lcm(a,b) = ab if and only if a and b are relatively prime.
Note that we can use the first of these, and the Euclidean algorithm, to find the least common multiple without
factoring. However, if we know the prime factorization of a is
![]() ,
and that of b is
,
and that of b is
![]() , then lcm(a,b) is
, then lcm(a,b) is
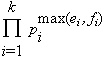 .
.
We can generalize gcd(a,b).lcm(a,b) = ab to three variables in a number of ways:
- gcd(a,b,c).lcm(ab,ac,bc) = abc
- lcm(a,b,c).gcd(ab,ac,bc) = abc
- gcd(lcm(a,b),lcm(a,c),lcm(b,c)) = lcm(gcd(a,b), gcd(a,c),gcd(b,c))
Finally, as a direct result of the properties of min and max functions we have the dual relations:
- gcd(a, lcm(b,c)) = lcm(gcd(a,b),gcd(a,c))
- lcm(a, gcd(b,c)) = gcd(lcm(a,b),lcm(a,c))
See Also: GCD
Printed from the PrimePages <t5k.org> © Reginald McLean.