hypothesis H
In 1958 Schinzel and Sierpinski proposed the following generalization of Dickson's conjecture.
- Conjecture (Hypothesis H)
- Let k be a positive integer and let f1(x), f2(x), . . ., fk(x) be irreducible polynomials with integral coefficients and positive leading coefficients. Assume also that there is not a prime p which divides the product f1(m).f2(m). . . . . fk(m) for every integer m. Then there exists a positive integer n such that f1(n), f2(n), . . ., fk(n) are all primes.
If there one such n making these polynomials all prime, then there are infinitely many such n. So, for example, this conjecture implies there are infinitely many primes of the form n2+1.
Hypothesis H was quantified as follows by Bateman and Horn in 1962. Let di be the degree of fi. For each prime p, let w(p) be the number of solutions to
f1(n).f2(n). . . . . fk(n) ≡ 0 (mod p)
then the expected number of values of n less than
N for which f1(n), f2(n), . . ., fk(n) are simultaneously prime, is
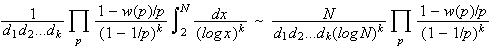 .
.
References:
- BH62
- P. T. Bateman and R. A. Horn, "A heuristic asymptotic formula concerning the distribution of prime numbers," Math. Comp., 16 (1962) 363-367. MR 26:6139
- Ribenboim95 (chapter 6, section IV)
- P. Ribenboim, The new book of prime number records, 3rd edition, Springer-Verlag, New York, NY, 1995. pp. xxiv+541, ISBN 0-387-94457-5. MR 96k:11112 [An excellent resource for those with some college mathematics. Basically a Guinness Book of World Records for primes with much of the relevant mathematics. The extensive bibliography is seventy-five pages.]
- SS58
- A. Schinzel and W. Sierpinski, "Sur certaines hypotheses concernment les nombres premiers," Acta. Arith., 4 (1958) 185-208. Erratum 5 (1958).
Printed from the PrimePages <t5k.org> © Reginald McLean.