prime number theorem
The ancient Greeks proved (about 300 BC) that there were infinitely many primes. About a century ago, it was shown thatthe number of primes not exceeding x (calledThis result is called the prime number theorem. We can state this in a more precise form using Riemann's Li function,) is asymptotic to x/log x.
for some constant a.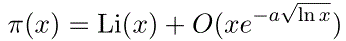
The prime number theorem implies that the probability that a random number n is prime, is about 1/log n (technically, the probability a number m chosen from the set {1,2,...,n} is prime is asymptotic to 1/log n). It also imples that the average gap between primes near n is about log n and that log (n#) is about n (n# is the primorial function).
See the document "How Many?" (linked below) for much more information on the prime number theorem and its history.
It is surprisingly difficult to give a reasonable heuristic argument for the prime number theorem (and not coincidentally, the proof of this theorem is rather involved). Greg Martin suggested the following approach. Suppose there is a function f(x) which is the "probability" that the integer x is prime. The integer x is prime with probability f(x), and then divides the larger integers with probability 1/x; so as x changes from x to x+1, f(x) changes to (roughly)
f(x).(1-f(x)/x).So we have
f '(x) = - f2(x)/x.The general solution of this differential equation is 1/(log(x) + c). This is a version of the prime number theorem (and the best choice of c is negative one).
See Also: PrimeGaps
Related pages (outside of this work)
- How many? (an in depth look at the prime number theorem)
- Proofs that there are infinitely many primes
- How big of an infinity?