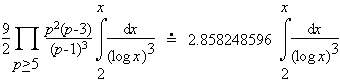The Prime Glossary: prime triple

prime triple
(another Prime Pages' Glossary entries)

Glossary:

Prime Pages:

Top 5000:

A prime triple is three consecutive primes, such that the first and the last differ by six. For example:

(5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (17, 19, 23), (37, 41, 43), (41, 43, 47), (67, 71, 73), (97, 101, 103), and (101, 103, 107).

It is conjectured that there are infinitely many such primes. In fact the Hardy-Littlewood prime k-tuple conjecture suggests that the number less than x of each of the forms

(p, p+2, p+6) and
(p, p+4, p+6)

is approximately

The actual numbers less than 100,000,000 are 55,600 and 55,556 respectively. The Hardy-Littlewood estimate above is 55,490.

See Also: PrimeConstellation, TwinPrime, Quadruple

Related pages (outside of this work)

Prime k-tuplets (includes the largest known prime triples)

References:

Riesel94
H. Riesel, Prime numbers and computer methods for factorization, Progress in Mathematics Vol, 126, Birkhäuser Boston, Boston, MA, 1994. ISBN 0-8176-3743-5. MR 95h:11142 [An excellent reference for those who want to start to program some of these algorithms. Code is provided in Pascal. Previous edition was vol. 57, 1985.]