Riemann zeta function
Riemann extended the definition of Euler's zeta function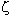 (s) to all complex
numbers s (except the simple pole at s=1
with residue one).
Euler’s product definition of this function still holds if
the real part of s is greater than one. To help
understand the values for other complex numbers, Riemann
derived the functional equation of the Riemann zeta
function:
(s) to all complex
numbers s (except the simple pole at s=1
with residue one).
Euler’s product definition of this function still holds if
the real part of s is greater than one. To help
understand the values for other complex numbers, Riemann
derived the functional equation of the Riemann zeta
function:
where the gamma function![[Functional Eq]](/gifs/zeta_eq.gif)
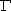 (s) is
the well-known extension of the factorial function (
(s) is
the well-known extension of the factorial function (Here the integral holds if the real part of s is greater than one, and the product holds for all complex numbers s.![[def of gamma]](/gifs/gammadef.gif)
See Also: RiemannHypothesis, EulerZetaFunction
Related pages (outside of this work)
- The Riemann hypothesis with expanded information on this function
Printed from the PrimePages <t5k.org> © Reginald McLean.