There are infinitely many primes. How big of an infinity?
Contents:
- Introduction - What is the question?
- Countability (is there another way to distinguish infinite sets?)
- Convergence and Divergence (definitions and examples)
- The Sum of the Reciprocal of the Primes (diverges! but for the twin primes...)
![[up]](gifs/up.gif) 1. Introduction -- What is the Question?
1. Introduction -- What is the Question?
About 2300 years ago Euclid proved that there were infinitely many primes. For mathematicians "infinitely many" is an incomplete answer--they then ask "how big of an infinity?" The prime number theorem, which states the number of primes less than x is approximately x/log x (the natural log), gives perhaps the best answer. Another way to answer that question is to ask whether or not the sum of the inverses of the primes converges--that is, what happens when we add up the following fractions?
1 1 1 1 1 1 1 1 1 - + - + - + - + -- + -- + -- + -- + -- + . . . 2 3 5 7 11 13 17 19 23
If you understand the terms convergence and divergence, then jump to section four below.
![[up]](gifs/up.gif) 2. Countability
2. Countability
In the field of real analysis we define two sets to be equivalent if there is a one to one correspondence between their elements (that is, if we can pair them up). Sets equivalent to the positive integers are said to be countable. For example, the primes are countable because we can pair 1 with the first prime, 2 with the second,...
Similarly all infinite subsets of the integers are countable sets--so this notion does not help us much!
![[up]](gifs/up.gif) 3. Convergence and Divergence
3. Convergence and Divergence
When dealing with an infinite set of positive integers for which we want some measure of its size we often look at the sum of the reciprocals. For example, consider the sum of the reciprocals of the squares:
As we add up more and more terms of this series, the sum gets arbitrarily
close to 
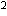 /6
(here
/6
(here  is the ratio of the circumference to the diameter
of a circle). So we say the series converges to
is the ratio of the circumference to the diameter
of a circle). So we say the series converges to 
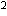 /6.
/6.
For a second example consider the series
This series clearly converges to one.
Next, consider the sum of the reciprocals of the positive integers (this is called the harmonic series):
As we add up more and more terms of this series the sum just keep getting larger--larger than any predetermined constant. (So if we add enough terms the sum is larger than 10, larger than 1010, larger than 101000000...). When this happens we say the series diverges.
If you have trouble seeing that the harmonic series diverges, think of it this way:
= ( 1/1 ) + ( 1/2 ) + ( 1/3 + 1/4 ) + ( 1/5 + 1/6 + 1/7 + 1/8 ) + ...
(where each set of parenthesis stops at a reciprocal of a power of two.) Replacing the terms in each set of parenthesis by the smallest term (in those parenthesis) we get a smaller sum:
> ( 1/1 ) + ( 1/2 ) + ( 1/4 + 1/4 ) + ( 1/8 + 1/8 + 1/8 + 1/8 ) + ...
= 1/1 + 1/2 + 1/2 + 1/2 + 1/2 + ...
which clearly gets arbitrarily large!
![[up]](gifs/up.gif) 4. The Sum of the Reciprocal of the Primes
4. The Sum of the Reciprocal of the Primes
When the sums of the reciprocals of a set of positive integers converge (example: the square integers), we think of that set as "small." When it diverges (example: the positive integers) we think of that set as "larger." So what about the set of primes?
We will show below that the sum of the reciprocals of the primes diverges, so the primes are a "large" subset of the integers. This is a simple consequence of the prime number theorem, but much more elementary proofs are available (e.g., [Ribenboim88 pp. 156-7]). On the other hand, it is conjectured that there are infinitely many twin primes (this is the twin prime conjecture, most everybody believes it is true--we just do not have a proof yet). Nevertheless, it has been proven the sum of the reciprocals of the twin primes is about is 1.90216054...(this is called Brun's constant). So the twin primes are only a "small" subset of the integers (in this sense).
To see the sum of the reciprocals of the primes diverge we will follow [HW79 p16-17] and start by bounding N(x) which is the number of positive integers n less than x which are divisible only by primes among the first i primes. We can write any such n as k.m2 where k is square free. Since there are just i primes which could divide k, we know there are exactly 2i choices of k (each of the i primes is either used or it is not). Also m2 < n < x, so we have N(x) < sqrt(x).2i.
Now suppose the sum of the reciprocals of the primes converges, then there is an integer i such that remainder after the first i terms (the "tail" of the series) is less than one half:
1 1 1 1 1 ---- + ---- + ---- + ---- + . . . < - . p p p p 2 i+1 i+2 i+3 i+4
(The denominators here are the i+1st prime, i+2nd prime and so on). The number of positive integers n less than x which are divisible by p is at most x/p, hence those divisible by any prime other than the first i primes, x - N(x), is at most
x x x x x ---- + ---- + ---- + ---- + . . . < - . p p p p 2 i+1 i+2 i+3 i+4
This gives N(x) > x/2. Combining this with our upper bound on N(x) we have
But this is false for all x larger than 22i+2, completing the proof.
It is interesting to note that there is a good bound for the partial sums of the reciprocals of the primes. If we let S(x) = the sum of the reciprocals of the primes less than x, then for x > 1,
where B is Euler's γ plus the sum over the primes p of (1/p + log(1-1/p)) [BS96, Thm 8.8.5]. B is about 0.261497.