Dirichlet's Theorem on Primes in Arithmetic Progressions
By Chris Caldwell
Often we are asked a question starting "are there any primes of the form ... ?" One of the classic ways to finish that question is "ak+l" where k and l are fixed integers, and a takes on the values 0, 1, 2, ... . For example, if k is 4 and l is 1, we are asking are there infinitely many primes in the following list?
We see several already, so we might guess that there are. But what if k is 4 and l is 2, then we are asking are there infinitely many primes in the following list? t
Obviously not! In fact it is a trivial exercise to prove that if there is more than one prime in the arithmetic sequence generated by k and l:
then k and l, are relatively prime (i.e., there is no positive integer that divides both k and l except 1). But is this relatively prime condition enough to guarentee infinitely many primes? Dirichlet answered yes over 150 years ago by proving the following.
Dirichlet's Theorem on Primes in Arithmetic Progressions (1837)If k and l are relatively prime positive integers, then the arithmetic progression
l, l+k, l+2k, l+3k, ...contains infinitely many primes.
Often knowing that there are infinitely many primes is enough, but sometimes we need more information--perhaps an estimate of how many are less than or equal to n for any given n (such as the prime number theorem gives in the case k=1). When the prime number theorem was proved, it then followed that
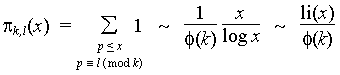
It is possible to give error estimates such as the following.
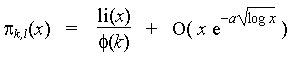
This was proved, for example, with a=1/15 [Walfisz63].