Home
Search Site
Largest
Finding
How Many?
Mersenne

Glossary
Prime Curios!
e-mail list
FAQ
Prime Lists
Titans
Submit primes
|
This is the Prime Pages'
interface to our BibTeX database. Rather than being an exhaustive database,
it just lists the references we cite on these pages. Please let me know of any errors you notice.References: [ Home | Author index | Key index | Search ]
- IS2003
- D. E. Iannucci and R. M. Sorli, "On the total number of prime factors of an odd perfect number," Math. Comp., 72:244 http://www.ams.org/jourcgi/jour-getitem?pii=S0025-5718-03-01522-9, (2003) 2077--2084. MR 1986824
Abstract:
We say n∈ N is perfect if σ(n)=2n, where σ(n) denotes the sum of the positive divisors of n. No odd perfect numbers are known, but it is well known that if such a number exists, it must have prime factorization of the form n=pα∏j=1kqj2βj, where p, q1, ..., qk are distinct primes and p≡α≡1 (mod 4) . We prove that if βj≡1 (mod 3) or βj≡2 (mod 5) for all j, 1≤ j≤ k, then 3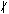 n. We also prove as our main result that Ω(n)≥37, where Ω(n)=α+2∑j=1kβj. This improves a result of Sayers (Ω(n)≥ 29) given in 1986. n. We also prove as our main result that Ω(n)≥37, where Ω(n)=α+2∑j=1kβj. This improves a result of Sayers (Ω(n)≥ 29) given in 1986.
|

