 |
Sophie Germain (p)
|
The Prime Pages keeps a list of the 5000 largest
known primes, plus a few each of certain selected archivable forms and
classes. These forms are defined in this collection's home page.This page is about one of those forms.
Definitions and Notes
If both p and 2p+1 are prime, then
p is a Sophie Germain prime.
The first few Sophie Germain primes are 2, 3, 5, 11,
23, 29, 41, 53, 83, 89, 113, and 131. Around 1825 Sophie
Germain proved that the first case of Fermat's Last
Theorem is true for such primes. Soon after Legendre
began to generalize this by showing the first case of
FLT also holds for odd primes p such that
kp+1 is prime, k=4, 8, 10, 14 and 16.
In 1991 Fee and Granville [FG91]
extended this to k<100, k not
a multiple of three. Many similar results were
also shown, but now that Fermat's Last Theorem
has been proven by Wiles, they are of less
interest.
Are there infinitely many Sophie Germain primes?
Ribenboim indicates that the sieve methods of Brun
(see the twin primes page) can be
used to estimate that the number of primes p <
x for
which kp+a is prime is bounded above by
C x/(log x)2
(so they have density zero among the primes).
Heuristically, it seems reasonable to conjecture
that there is a lower bound of this form as well.
More specifically (see
a simple
heuristic), it is conjectured that the number of
Sophie Germain primes less than
N is asympototic to
where C2 is the twin
prime constant (estimated by Wrench and others to
be approximately 0.6601618158...).
This estimate works suprisingly well! For example: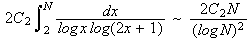
The number of Sophie Germain
primes less than N
| N | actual | estimate |
|---|
| 1,000 | 37 |
39 |
| 100,000 | 1171 |
1166 |
| 10,000,000 | 56032 |
56128 |
| 100,000,000 | 423140 |
423295 |
| 1,000,000,000 | 3308859 |
3307888 |
| 10,000,000,000 | 26569515 |
26568824 |
Euler and
Lagrange
proved that if we also have p ≡ 3
(mod 4) and p > 3, then
2p+1 is prime (and p is a Sophie Germain prime)
if and only if 2p+1
divides the Mersenne Mp.
(Thanks to Chip Kerchner for the last two entries in the table above.)
Record Primes of this Type
| rank | prime |
digits | who | when | comment |
|---|
| 1 | 2618163402417 · 21290000 - 1 |
388342 |
L927 |
Feb 2016 |
Sophie Germain (p) |
| 2 | 18543637900515 · 2666667 - 1 |
200701 |
L2429 |
Apr 2012 |
Sophie Germain (p) |
| 3 | 183027 · 2265440 - 1 |
79911 |
L983 |
Mar 2010 |
Sophie Germain (p) |
| 4 | 648621027630345 · 2253824 - 1 |
76424 |
x24 |
Nov 2009 |
Sophie Germain (p) |
| 5 | 620366307356565 · 2253824 - 1 |
76424 |
x24 |
Nov 2009 |
Sophie Germain (p) |
| 6 | 1068669447 · 2211088 - 1 |
63553 |
L4166 |
May 2020 |
Sophie Germain (p) |
| 7 | 99064503957 · 2200008 - 1 |
60220 |
L95 |
Apr 2016 |
Sophie Germain (p) |
| 8 | 12443794755 · 2184516 - 1 |
55555 |
L3494 |
Sep 2021 |
Sophie Germain (p) |
| 9 | 21749869755 · 2184515 - 1 |
55555 |
L3494 |
Sep 2021 |
Sophie Germain (p) |
| 10 | 14901867165 · 2184515 - 1 |
55555 |
L3494 |
Sep 2021 |
Sophie Germain (p) |
| 11 | 607095 · 2176311 - 1 |
53081 |
L983 |
Sep 2009 |
Sophie Germain (p) |
| 12 | 48047305725 · 2172403 - 1 |
51910 |
L99 |
Jan 2007 |
Sophie Germain (p) |
| 13 | 137211941292195 · 2171960 - 1 |
51780 |
x24 |
May 2006 |
Sophie Germain (p) |
| 14 | 4931286045 · 2152849 - 1 |
46022 |
L5389 |
Jul 2021 |
Sophie Germain (p) |
| 15 | 4318624617 · 2152849 - 1 |
46022 |
L5389 |
Jul 2021 |
Sophie Germain (p) |
| 16 | 21195711 · 2143630 - 1 |
43245 |
L3494 |
Jun 2019 |
Sophie Germain (p) |
| 17 | 838269645 · 2143165 - 1 |
43106 |
L3494 |
Jun 2019 |
Sophie Germain (p) |
| 18 | 570409245 · 2143163 - 1 |
43106 |
L3494 |
Jun 2019 |
Sophie Germain (p) |
| 19 | 2830598517 · 2143112 - 1 |
43091 |
L3494 |
Jul 2019 |
Sophie Germain (p) |
| 20 | 4158932595 · 2143073 - 1 |
43079 |
L3494 |
Jul 2019 |
Sophie Germain (p) |
|
Related Pages
References
- Agoh2000
- Agoh, Takashi, "On Sophie Germain primes," Tatra Mt. Math. Publ., 20 (2000) 65--73. Number theory (Liptovský Ján, 1999). MR 1845446
- CFJJK2006
- Csajbók, T., Farkas, G., Járai, A., Járai, Z. and Kasza, J., "Report on the largest known Sophie Germain and twin primes," Ann. Univ. Sci. Budapest. Sect. Comput., 26 (2006) 181--183. MR 2388687
- Dubner96
- H. Dubner, "Large Sophie Germain primes," Math. Comp., 65:213 (1996) 393--396. MR 96d:11008 (Abstract available)
- JR2007
- Jaroma, John H. and Reddy, Kamaliya N., "Classical and alternative approaches to the Mersenne and Fermat numbers," Amer. Math. Monthly, 114:8 (2007) 677--687. MR 2354438
- Peretti1987
- Peretti, A., "The quantity of Sophie Germain primes less than x," Bull. Number Theory Related Topics, 11:1-3 (1987) 81--92. MR 995537
- Ribenboim95
- P. Ribenboim, The new book of prime number records, 3rd edition, Springer-Verlag, New York, NY, 1995. pp. xxiv+541, ISBN 0-387-94457-5. MR 96k:11112 [An excellent resource for those with some college mathematics. Basically a Guinness Book of World Records for primes with much of the relevant mathematics. The extensive bibliography is seventy-five pages.]
- Yates1987
- Yates, Samuel, Sophie Germain primes. In "The mathematical heritage of C. F. Gauss," World Sci. Publ., River Edge, NJ, 1991. pp. 882--886, MR 1146271