Lehmer number

This page : Definition(s) | Records | References |

The Prime Pages

Let me know if something in the Top20 is not working (caldwell@utm.edu).

The Prime Pages keeps a list of the 5000 largest known primes, plus a few each of certain selected archivable forms and classes. These forms are defined in this collection's home page. This page is about one of those forms. Comments and suggestions requested.

Definitions and Notes

Lucas generalized the sequence of Fibonacci numbers as follows: let a and b be the zeros of the polynomial x²-Px+Q (where P, Q and D = P²-4Q are non-zero integers), then set

U_n(P,Q) = (aⁿ - bⁿ)/(a - b), and V_n(P,Q) = aⁿ + bⁿ.

Lehmer noted that we can loosen the restriction that P be an integer and still get a sequence of integers by replacing P with the squareroot of R and slightly modifying these definitions. To make sure the sequences are not zero infinitely often we require that a/b not be a root of unity:

These share many properties with the generalized Lucas numbers.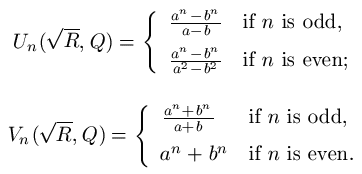

For integers P, the two numbers U_k+1(P,1) ± U_k(P,1) are Lehmer numbers whose product is equal to U_2k+1(P,1). This follows from the fact that when Q=1 we may write (P ± sqrt(P²-4Q))/2 as the square of (sqrt(P+2) ± sqrt(P-2))/2, and hence obtain Lehmer's sqrt(R) as sqrt(P+2).

Note that the Lehmer numbers U_k+1(P,1) ± U_k(P,1) cannot be prime if 2k+1 is composite.

Record Primes of this Type

rank prime digits who when comment

1 U(15694, 1, 14700) + U(15694, 1, 14699) 61674 x45 Aug 2019 Lehmer number
2 U(809, 1, 17325) - U(809, 1, 17324) 50378 x45 Jul 2019 Lehmer number
3 U(52245, 1, 9241) + U(52245, 1, 9240) 43595 x45 Jul 2019 Lehmer number
4 U(35896, 1, 7260) + U(35896, 1, 7259) 33066 x45 Jul 2019 Lehmer number
5 U(23396, 1, 6615) + U(23396, 1, 6614) 28898 x45 Jul 2019 Lehmer number
6 U(16531, 1, 6721) - U(16531, 1, 6720) 28347 x36 May 2007 Lehmer number
7 U(5092, 1, 7561) + U(5092, 1, 7560) 28025 x25 Oct 2014 Lehmer number
8 U(5239, 1, 7350) - U(5239, 1, 7349) 27333 CH10 Jun 2017 Lehmer number
9 U(1766, 1, 7561) - U(1766, 1, 7560) 24548 x25 Nov 2013 Lehmer number
10 U(1383, 1, 7561) + U(1383, 1, 7560) 23745 x25 Nov 2013 Lehmer number
11 U(1118, 1, 7561) - U(1118, 1, 7560) 23047 x25 Oct 2013 Lehmer number
12 U(43100, 1, 4620) + U(43100, 1, 4619) 21407 x25 Jun 2016 Lehmer number
13 U(15631, 1, 5040) - U(15631, 1, 5039) 21134 x25 Apr 2003 Lehmer number
14 U(35759, 1, 4620) + U(35759, 1, 4619) 21033 x25 May 2016 Lehmer number
15 U(31321, 1, 4620) - U(31321, 1, 4619) 20767 x25 Jun 2016 Lehmer number
16 U(22098, 1, 4620) + U(22098, 1, 4619) 20067 x25 Jun 2016 Lehmer number
17 U(21412, 1, 4620) - U(21412, 1, 4619) 20004 x25 Jun 2016 Lehmer number
18 U(19361, 1, 4620) + U(19361, 1, 4619) 19802 x25 May 2016 Lehmer number
19 U(9657, 1, 4321) - U(9657, 1, 4320) 17215 x23 Dec 2005 Lehmer number
20 U(15823, 1, 3960) - U(15823, 1, 3959) 16625 x25 Nov 2002 Lehmer number, cyclotomy

References

Gyory1982
Györy, K., "On some arithmetical properties of Lucas and Lehmer numbers," Acta Arith., 40:4 (1981/82) 369--373. MR667047
Gyory2003
Györy, K., "On some arithmetical properties of Lucas and Lehmer numbers. II," Acta Acad. Paedagog. Agriensis Sect. Mat. (N.S.), 30 (2003) 67--73. Dedicated to the memory of Professor Dr. P\'eter Kiss. MR2054716
LP2003
Luca, F. and Porubský, S., "The multiplicative group generated by the Lehmer numbers," Fibonacci Quart., 41:2 (2003) 122--132. MR1990520
McDaniel1993
McDaniel, W., "Square Lehmer numbers," Colloq. Math., 66:1 (1993) 85--93. MR1242648
Ribenboim95
P. Ribenboim, The new book of prime number records, 3rd edition, Springer-Verlag, New York, NY, 1995. pp. xxiv+541, ISBN 0-387-94457-5. MR 96k:11112 [An excellent resource for those with some college mathematics. Basically a Guinness Book of World Records for primes with much of the relevant mathematics. The extensive bibliography is seventy-five pages.]
RW1980
Rotkiewicz, A. and Wasén, R., "Lehmer's numbers," Acta Arith., 36:3 (1980) 203--217. MR581371
Schinzel1962
Schinzel, A., "On primitive prime factors of Lehmer numbers. I," Acta. Arith., 8 (1962/1963) 213--223. MR 27:1408
Schinzel1962b
Schinzel, A., "The intrinsic divisors of Lehmer numbers in the case of negative discriminant," Ark. Mat., 4 (1962) 413--416 (1962). MR0139567
Schinzel1963
Schinzel, A., "On primitive prime factors of Lehmer numbers. II," Acta. Arith., 8 (1962/1963) 251--257. MR 27:1409
Schinzel1968
Schinzel, A., "On primitive prime factors of Lehmer numbers. III," Acta Arith., 15 (1968) 49--70. MR0232744
SS1981
Shorey, T. N. and Stewart, C. L., "On divisors of Fermat, Fibonacci, Lucas and Lehmer numbers. II," J. London Math. Soc. (2), 23:1 (1981) 17--23. MR 82m:10025
Stewart1976
Stewart, C. L., Primitive divisors of Lucas and Lehmer numbers. In "Transcendence theory: advances and applications (Proc. Conf., Univ. Cambridge, Cambridge, 1976)," Academic Press, 1977. London, pp. 79--92, MR0476628
Stewart1977
C. L. Stewart, "On divisors of Fermat, Fibonacci, Lucas and Lehmer numbers," Proc. Lond. Math. Soc., 35:3 (1977) 425--447. MR 58:10694
Stewart1983
Stewart, C. L., "On divisors of Fermat, Fibonacci, Lucas and Lehmer numbers. III," J. London Math. Soc. (2), 28:2 (1983) 211--217. MR 85g:11021
Ward1955
Ward, M., "The intrinsic divisors of Lehmer numbers," Ann. of Math. (2), 62 (1955) 230--236. MR0071446