Fermat Divisors

The Prime Pages keeps a list of the 5000 largest known primes, plus a few each of certain selected archivable forms and classes. These forms are defined in this collection's home page.

This page is about one of those forms.

Definitions and Notes

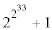The Fermat primes are the primes of the form 2^2ⁿ+1 for non-negative integers n. Only five Fermat primes are known (n=0, 1, 2, 3, 4), and the Fermat numbers grow so quickly that it may be many years before the first undecided case: F₃₃ = 2^2^33+1

(a number with over 2.5 billion digits!) is shown prime or composite--unless we luck onto a divisor. So every since Euler found the first Fermat divisor (non-trivial divisor of a Fermat composite), factorers have been collecting these rare numbers.

Euler showed that that every divisor of F_n (n greater than 2) must have the form k^.2ⁿ⁺²+1 for some integer k. For this reason, when we find a large prime of the form k^.2ⁿ+1 (with k small), we usually check to see if it divides a Fermat number. (For example, Gallot's Win95 program Proth.exe has this test built in.)

Record Primes of this Type

rank prime digits who when comment

1 7 · 2^18233956 + 1 5488969 L4965 Oct 2020 Divides Fermat F(18233954)
2 27 · 2^7963247 + 1 2397178 L5161 Jan 2021 Divides Fermat F(7963245)
3 13 · 2^5523860 + 1 1662849 L1204 Jan 2020 Divides Fermat F(5523858)
4 193 · 2^3329782 + 1 1002367 L3460 Jul 2014 Divides Fermat F(3329780)
5 57 · 2^2747499 + 1 827082 L3514 May 2013 Divides Fermat F(2747497)
6 267 · 2^2662090 + 1 801372 L3234 Feb 2015 Divides Fermat F(2662088)
7 9 · 2^2543551 + 1 765687 L1204 Jun 2011 Divides Fermat F(2543548), GF(2543549, 3), GF(2543549, 6), GF(2543549, 12)
8 3 · 2^2478785 + 1 746190 g245 Oct 2003 Divides Fermat F(2478782), GF(2478782, 3), GF(2478776, 6), GF(2478782, 12)
9 7 · 2^2167800 + 1 652574 g279 Apr 2007 Divides Fermat F(2167797), GF(2167799, 5), GF(2167799, 10)
10 3 · 2^2145353 + 1 645817 g245 Feb 2003 Divides Fermat F(2145351), GF(2145351, 3), GF(2145352, 5), GF(2145348, 6), GF(2145352, 10), GF(2145351, 12)
11 25 · 2^2141884 + 1 644773 L1741 Sep 2011 Divides Fermat F(2141872), GF(2141871, 5), GF(2141872, 10); generalized Fermat
12 183 · 2^1747660 + 1 526101 L2163 Mar 2013 Divides Fermat F(1747656)
13 131 · 2^1494099 + 1 449771 L2959 Feb 2012 Divides Fermat F(1494096)
14 329 · 2^1246017 + 1 375092 L2085 Jan 2012 Divides Fermat F(1246013)
15 2145 · 2^1099064 + 1 330855 L1792 Jun 2013 Divides Fermat F(1099061)
16 11 · 2⁹⁶⁰⁹⁰¹ + 1 289262 g277 Feb 2005 Divides Fermat F(960897)
17 1705 · 2⁹⁰⁶¹¹⁰ + 1 272770 L3174 Jun 2012 Divides Fermat F(906108)
18 27 · 2⁶⁷²⁰⁰⁷ + 1 202296 g279 Aug 2005 Divides Fermat F(672005)
19 659 · 2⁶¹⁷⁸¹⁵ + 1 185984 L732 Apr 2009 Divides Fermat F(617813)
20 151 · 2⁵⁸⁵⁰⁴⁴ + 1 176118 L446 Mar 2007 Divides Fermat F(585042)

Weighted Record Primes of this Type

For purposes of amusement only, we decided to try to rank these divisors based on the facts that (1) large primes are harder to find than small ones; and (2) the probability that N = k2ⁿ+1 divides a Fermat numbers appears to be O(1/k). (Note that all primes have this form!)

More specifically, the number of operations to prove N is prime is O(ln³N ln ln N). So to N = k2ⁿ+1 we might assign the weight

k ln³N ln ln N

To make these weights smaller we take the log this expression.

ln k + 3 ln ln N + ln ln ln N

Yves Gallot interprets this to suggest that if you want to find a Fermat factor, use a small n. If you want to find a record sized factor, use a small k.

rank prime digits who when comment

1 7 · 2^18233956 + 1 5488969 L4965 Oct 2020 Divides Fermat F(18233954)
2 27 · 2^7963247 + 1 2397178 L5161 Jan 2021 Divides Fermat F(7963245)
3 193 · 2^3329782 + 1 1002367 L3460 Jul 2014 Divides Fermat F(3329780)
4 267 · 2^2662090 + 1 801372 L3234 Feb 2015 Divides Fermat F(2662088)
5 2145 · 2^1099064 + 1 330855 L1792 Jun 2013 Divides Fermat F(1099061)
6 13 · 2^5523860 + 1 1662849 L1204 Jan 2020 Divides Fermat F(5523858)
7 57 · 2^2747499 + 1 827082 L3514 May 2013 Divides Fermat F(2747497)
8 1705 · 2⁹⁰⁶¹¹⁰ + 1 272770 L3174 Jun 2012 Divides Fermat F(906108)
9 183 · 2^1747660 + 1 526101 L2163 Mar 2013 Divides Fermat F(1747656)
10 329 · 2^1246017 + 1 375092 L2085 Jan 2012 Divides Fermat F(1246013)
11 131 · 2^1494099 + 1 449771 L2959 Feb 2012 Divides Fermat F(1494096)
12 25 · 2^2141884 + 1 644773 L1741 Sep 2011 Divides Fermat F(2141872), GF(2141871, 5), GF(2141872, 10); generalized Fermat
13 9 · 2^2543551 + 1 765687 L1204 Jun 2011 Divides Fermat F(2543548), GF(2543549, 3), GF(2543549, 6), GF(2543549, 12)
14 659 · 2⁶¹⁷⁸¹⁵ + 1 185984 L732 Apr 2009 Divides Fermat F(617813)
15 7 · 2^2167800 + 1 652574 g279 Apr 2007 Divides Fermat F(2167797), GF(2167799, 5), GF(2167799, 10)
16 3 · 2^2478785 + 1 746190 g245 Oct 2003 Divides Fermat F(2478782), GF(2478782, 3), GF(2478776, 6), GF(2478782, 12)
17 3 · 2^2145353 + 1 645817 g245 Feb 2003 Divides Fermat F(2145351), GF(2145351, 3), GF(2145352, 5), GF(2145348, 6), GF(2145352, 10), GF(2145351, 12)
18 151 · 2⁵⁸⁵⁰⁴⁴ + 1 176118 L446 Mar 2007 Divides Fermat F(585042)
19 11 · 2⁹⁶⁰⁹⁰¹ + 1 289262 g277 Feb 2005 Divides Fermat F(960897)
20 27 · 2⁶⁷²⁰⁰⁷ + 1 202296 g279 Aug 2005 Divides Fermat F(672005)

Status of the factorization of Fermat numbers
The Prime Glossary's: Fermat divisor

References

AB1986
Akushskii, I. Ya. and Burtsev, V. M., "Realization of primality tests for Mersenne and Fermat numbers," Vestnik Akad. Nauk Kazakh. SSR,:1 (1986) 52--59. MR 843070
BLSTW88
J. Brillhart, D. H. Lehmer, J. L. Selfridge, B. Tuckerman and S. S. Wagstaff, Jr., Factorizations of bⁿ ± 1, b=2,3,5,6,7,10,12 up to high powers, Amer. Math. Soc., Providence RI, 1988. pp. xcvi+236, ISBN 0-8218-5078-4. MR 90d:11009 (Annotation available)
Brent1982
Brent, Richard P., "Succinct proofs of primality for the factors of some Fermat numbers," Math. Comp., 38:157 (1982) 253--255. (http://dx.doi.org/10.2307/2007482) MR 637304
DK95
H. Dubner and W. Keller, "Factors of generalized Fermat numbers," Math. Comp., 64 (1995) 397--405. MR 95c:11010
KLS2001
M. Krízek, F. Luca and L. Somer, 17 lectures on Fermat numbers: from number theory to geometry, CMS Books in Mathematics Vol, 9, Springer-Verlag, New York, NY, 2001. pp. xvii + 257, ISBN 0-387-95332-9. MR 2002i:11001
McIntosh1983
McIntosh, Richard, "A necessary and sufficient condition for the primality of Fermat numbers," Amer. Math. Monthly, 90:2 (1983) 98--99. (http://dx.doi.org/10.2307/2975806) MR 691180

Fermat Divisors

Definitions and Notes

Record Primes of this Type

Weighted Record Primes of this Type

Related Pages

References