floor function
The floor function of x, historically called the greatest integer function, is the greatest integer less than or equal to x. This function is sometimes written [x], but is best written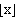 (a notation that was suggested by Iverson in 1962) to differentiate it from the ceiling function.
(a notation that was suggested by Iverson in 1962) to differentiate it from the ceiling function.
Examples: [3.14159]=3, [-3.14159]=-4, and [log(n)/log(10)]+1 is the number of digits in the decimal expansion of the positive integer n.
See Also: CeilingFunction
References:
- Iverson62
- K. E. Iverson, A programming language, John Wiley \& Sons, 1962. MR 26:913
Printed from the PrimePages <t5k.org> © Reginald McLean.