Cunningham chain
Recall that a Sophie Germain prime is a prime p such that q=2p+1 is also prime. Why not also ask that r=2q+1 is prime, and 2r+1 is prime, and...? A Cunningham chain of length k (of the first kind) is sequence of k primes, each which is twice the preceding one plus one. For example, {2, 5, 11, 23, 47} and {89, 179, 359, 719, 1439, 2879}.A Cunningham chain of length k (of the second kind) is a sequence of k primes, each which is twice the preceding one minus one. (For example, {2, 3, 5} and {1531, 3061, 6121, 12241, 24481}.)
Primes of both these forms are called complete chains if they can not be extended by adding either the next larger, or smaller, terms. In the following table (from [Loh89]) we list the first complete chains for several lengths.
Prime at which the first complete chain starts length first kind second kind 1 13 11 2 3 7 3 41 2 4 509 2131 5 2 1531 6 89 385591 7 1122659 16651 8 19099919 15514861 9 85864769 857095381 10 26089808579 205528443121 11 665043081119 1389122693971 12 554688278429 216857744866621 13 4090932431513069 758083947856951
How long can these chains get? The prime k-tuple conjecture implies that there should be infinitely many for each of these primes. In fact, the number less than x should be asymptotic to
where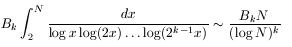
The sequence Bk begins approximately 1.32032 (k=2), 2.85825, 5.553491, 20.2636, 71.9622, 233.878, 677.356.
Tony Forbes has found chains of length 14 (for the first kind) and 16 (for the second kind). See the links below for current records.
Note that some authors extend the definition of Cunningham Chain to all sequences of primes pi the form pi+1 = api+b where a and b are fixed, relatively prime integers with a > 1.
Related pages (outside of this work)
- The Twenty largest Cunningham Chains of the first kind
- The Twenty largest Cunningham Chains of the second kind
References:
- Cunningham1907
- A. Cunnningham, "On hyper-even numbers and on Fermat's numbers," Proc. Lond. Math. Soc., series 2, 5 (1907) 237--274.
- Guy94 (SectionA7)
- R. K. Guy, Unsolved problems in number theory, Springer-Verlag, 1994. New York, NY, ISBN 0-387-94289-0. MR 96e:11002 [An excellent resource! Guy briefly describes many open questions, then provides numerous references. See his newer editions of this text.]
- Lehmer1965
- D. H. Lehmer, "On certain chains of primes," Proc. Lond. Math. Soc., series 3, 14a (1965) 183--186. MR 31:2222
- Loh89
- G. Löh, "Long chains of nearly doubled primes," Math. Comp., 53 (1989) 751-759. MR 90e:11015 (Abstract available) [Chains of primes for which each is either twice the proceeding one plus one, or each is either twice the proceeding one minus one. See also [Guy94, section A7].]
- Ribenboim95 (p 333)
- P. Ribenboim, The new book of prime number records, 3rd edition, Springer-Verlag, New York, NY, 1995. pp. xxiv+541, ISBN 0-387-94457-5. MR 96k:11112 [An excellent resource for those with some college mathematics. Basically a Guinness Book of World Records for primes with much of the relevant mathematics. The extensive bibliography is seventy-five pages.]
- Yates82
- S. Yates, Repunits and repetends, Star Publishing Co., Inc., Boynton Beach, Florida, 1982. pp. vi+215, MR 83k:10014