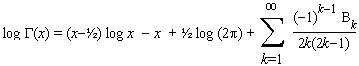Stirling's formula
(another Prime Pages' Glossary entries)
The Prime Glossary
Glossary: Prime Pages: Top 5000: Stirling found the following formula for approximating factorials:
n! ~ !=(n/e)^n sqrt(2 pi n)
and more precisely,
n!=(n/e)^n sqrt(2 pi n) e^(theta(n)/12n)
where 0 < theta < 1 (and e is the base of the natural logarithms). In terms of the gamma function Stirling's formula is
a ugly formula
and
another ugly one
where Bk is the kth Bernoulli number.

References:

AS1974
M. Abramowitz and I. Stegun editors, Handbook of mathematical functions--with formulas, graphs, and mathematical tables, Dover Pub., New York, NY, 1974.  pp. xiv+1046, ISBN 0-486-61272-4. MR 94b:00012


Chris K. Caldwell © 1999-2013 (all rights reserved)