Twin
primes are pairs of primes which differ by two.
The first
twin primes are {3,5}, {5,7}, {11,13} and {17,19}.
It has been
conjectured
(but never proven) that there are infinitely many twin
primes.
If the probability of
a random
integer n and the integer
n+2 being prime were statistically independent
events, then it would follow from the
prime number theorem that there are about
n/(
log n)
2 twin primes less
than or equal to
n. These probabilities are not
independent, so Hardy and Littlewood
conjectured that the correct estimate should be the following.
Here the
infinite product is the
twin
prime constant (estimated by Wrench and others to
be approximately 0.6601618158...), and we introduce an integral
to improve the quality of the estimate.
This estimate works quite well! For example: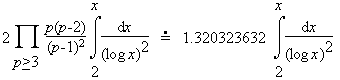
The number of twin primes
less than N
| N | actual | estimate |
|---|
| 106 | 8169 |
8248 |
| 108 | 440312 |
440368 |
| 1010 | 27412679 |
27411417 |
There is a longer table by Kutnib
and Richstein available online.
In 1919 Brun showed that the sum of the
reciprocals of the twin primes converges to a sum now called
Brun's Constant.
(Recall that the sum of the
reciprocals of all primes diverges.) By calculating the twin primes up to
1014 (and discovering the infamous pentium bug along the way),
Thomas Nicely heuristically
estimates Brun's constant to be 1.902160578.
As an exercise you might want to prove the following
version of Wilson's theorem.
- Theorem: (Clement 1949)
- The integers n, n+2, form a pair of twin
primes if and only if
4[(n-1)!+1] 
-n (mod n(n+2)).
Nice--too bad it is of virtually no practical value!
Definitions and Notes