The Top Twenty--a Prime Page Collection

Arithmetic Progressions of Primes

This page : Definition(s) | Records | Weighted Records | References | Related Pages |

The Prime Pages

The Prime Pages keeps a list of the 5000 largest known primes, plus a few each of certain selected archivable forms and classes. These forms are defined in this collection's home page. This page is about one of those forms. Comments and suggestions requested.

Definitions and Notes

Are there infinitely many primes in most arithmetic progressions? Certainly not if the common difference has a prime factor in common with one of the terms (for example: 6, 9, 12, 15, ...). In 1837, Dirichlet proved that in all other cases the answer was yes:

Dirichlet's Theorem on Primes in Arithmetic Progressions
If a and b are relatively prime positive integers, then the arithmetic progression a, a+b, a+2b, a+3b, ... contains infinitely many primes.

Recall that the prime number theorem states that for any given n, there are asymptotically n/log n primes less than n. Similarly it can be proven that the sequence a + k*b (k = 1,2,3,...) contains asymptotically n/(phi(b) log n) primes less than n. This estimate does not depend on the choice of a!

Dirichlet's theorem does not say that there are arbitrarily many consecutive terms in this sequence which are primes (which is what we'd like). But Dickson's conjecture does suggests that given any positive integer n, then for each "acceptable" arithmetic progression there are n consecutive terms which are prime. In 1939, van der Corput showed that there are infinitely many triples of primes in arithmetic progression [Corput1939]. In 2004, Green and Tao [GT2004a] showed that there are indeed arbitrarily long sequences of primes and that a k-term sequence of primes occurs before [GT2004b]:

2^{2^{2^{2^{2^{2^{2^{2^100k}}}}}}}

Obviously this is not optimal! It is conjectured that it actually occurs before k!+1.

But either way, there is a world of difference betwen what we know to be true (there are infinitely long arithemetic progressions of primes), and what we have computed: the longest is just over two dozent terms! (See Jens Kruse Andersen's excellent pages linked below.)

It is also possible to put this into a quantative form and heuristically estimate how many there should be. For example, Grosswald [GH79] suggested that if N_k is the number of arithmetic progressions of k primes all less than N, then

where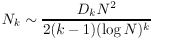

He was able to prove this for the case k=3 [GH79]. Green and Tao have recently proven it for k=4 [GT2006a].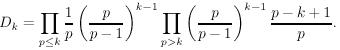

In our heuristics pages we also give asymptotic estimates for the number with fixed length k and fixed difference d. The first table shows the largest known primes in arithmetic sequence (but just the third term and beyond for each sequence).

[ See all such primes on the list.]

Record Primes of this Type

rank prime digits who when comment

1 9094283341425 · 2⁶⁶⁶⁶⁶⁹ - 1 200701 p199 Mar 2011 term 3, difference 32289415560495 · 2⁶⁶⁶⁶⁶⁶
2 26767338410445 · 2⁶⁶⁶⁶⁶⁶ - 1 200700 p199 Mar 2011 term 3, difference 12521740750545 · 2⁶⁶⁶⁶⁶⁶
3 23716957113345 · 2⁶⁶⁶⁶⁶⁶ - 1 200700 p199 Feb 2011 term 3, difference 2697434638065 · 2⁶⁶⁶⁶⁶⁸
4 11638738675125 · 2⁶⁶⁶⁶⁶⁷ - 1 200700 p199 Mar 2011 term 3, difference 9571322415225 · 2⁶⁶⁶⁶⁶⁶
5 14646182194005 · 2⁶⁶⁶⁶⁶⁶ - 1 200700 p199 Mar 2011 term 3, difference 3388839720735 · 2⁶⁶⁶⁶⁶⁶
6 492590931 · 2⁸⁰⁰⁰⁰ - 1631979959 · 2²⁵⁰⁰¹ - 1 24092 p199 Oct 2010 term 4, difference 164196977 · 2⁸⁰⁰⁰⁰ - 1631979959 · 2²⁵⁰⁰⁰
7 1008075799 · 34687# + 1 15004 p252 Jul 2010 term 4, difference 2571033 · 34687#
8 263821581 · 2⁴⁵⁰⁰¹ - 487069965 · 2²⁵⁰⁰² - 1 13556 p199 Jun 2010 term 4, difference 87940527 · 2⁴⁵⁰⁰¹ - 487069965 · 2²⁵⁰⁰¹
9 4103163 · 2⁴⁵⁰⁰⁷ - 183009063 · 2²⁵⁰⁰³ - 1 13556 p199 Jun 2010 term 4, difference 1367721 · 2⁴⁵⁰⁰⁷ - 183009063 · 2²⁵⁰⁰²
10 664227 · 2⁴⁵⁰⁰¹ - 21037539 · 2²⁵⁰⁰⁶ - 1 13553 p199 Jun 2010 term 4, difference 221409 · 2⁴⁵⁰⁰¹ - 21037539 · 2²⁵⁰⁰⁵
11 197418203 · 2²⁵⁰⁰⁰ + 6089 7535 FE4 Feb 2005 ECPP, consecutive primes term 3, difference 6090
12 87 · 2²⁴⁵⁸² + 2579 7402 c31 Nov 2004 ECPP, consecutive primes term 3, difference 1290
13 164084347 · 16229# + 1 7009 p155 Mar 2009 term 5, difference 20333209 · 16229#
14 2852851249 · 16001#/5 + 1 6913 p199 Jun 2008 term 5, difference 2653152 · 16001#
15 2399771561 · 16001#/5 + 1 6913 p199 Jun 2008 term 5, difference 86574302 · 16001#
16 1638535589 · 16001#/5 + 1 6913 p199 Jun 2008 term 5, difference 2003735 · 16001#
17 4811 · 2²⁰²¹⁹ + 1 6091 DM Oct 1996 Consecutive primes term 3, difference 3738 [c36]
18 (84055657369 · 205881 · 4001# · (205881 · 4001# + 1) + 210) · (205881 · 4001# - 1)/35 + 13 5132 p179 Apr 2006 Consecutive primes term 3, difference 6
19 (61310346529 · 205881 · 4001# · (205881 · 4001# + 1) + 210) · (205881 · 4001# - 1)/35 + 13 5132 p179 Oct 2005 Consecutive primes term 3, difference 6
20 (51803036889 · 205881 · 4001# · (205881 · 4001# + 1) + 210) · (205881 · 4001# - 1)/35 + 7 5132 p179 Feb 2007 term 5, difference (681402540 · 205881 · 4001# · (205881 · 4001# + 1) · (205881 · 4001# - 1)/35)

Weighted Record Primes of this Type

The difficulty of finding such sequences depends on their length. For example, it will be a long time before a an arithmetic sequence of twenty titanic primes is known! Just for the fun of it, let's attempt to rank these sequences by how long they are.

To rank them, we might take the usual estimate of how hard it is to prove primality of a number the size of n

log(n)² log log n

and multiply it by the expected number of potential candidates to test before we find one of length k (by the heuristic estimate above):

sqrt(2(k-1)/D_k) (log n)^(2+k/2) log log n.

We then take the log one more time just to reduce the size of these numbers.

Notes:

We use the natural log in calculating this weight.
The D_k's begin 1.32032363, 2.85824860, 4.15118086, 10.1317949, 17.2986123, and 53.9719483 for k = 3, 4, 5, 6, 7, and 8. They continue 148.551629, 336.034327, 1312.31971, 2364.59896, 7820.60003, 22938.9086, 55651.4626, 91555.1112, 256474.860, 510992.010, 1900972.58, 6423764.31, 18606666.2, 38734732.7, 153217017., 568632503.5, 1941938595 ... [GH79].

rank prime digits who when comment

1 116040452086 · 2371# + 1 1014 p308 Jan 2012 term 9, difference 6317280828 · 2371#
2 97336164242 · 2371# + 1 1014 p308 Apr 2013 term 9, difference 6350457699 · 2371#
3 93537753980 · 2371# + 1 1014 p308 Apr 2013 term 9, difference 3388165411 · 2371#
4 92836168856 · 2371# + 1 1014 p308 Apr 2013 term 9, difference 127155673 · 2371#
5 69318339141 · 2371# + 1 1014 p308 Jul 2011 term 9, difference 1298717501 · 2371#
6 3124777373 · 7001# + 1 3019 p155 Feb 2012 term 7, difference 481789017 · 7001#
7 9094283341425 · 2⁶⁶⁶⁶⁶⁹ - 1 200701 p199 Mar 2011 term 3, difference 32289415560495 · 2⁶⁶⁶⁶⁶⁶
8 26767338410445 · 2⁶⁶⁶⁶⁶⁶ - 1 200700 p199 Mar 2011 term 3, difference 12521740750545 · 2⁶⁶⁶⁶⁶⁶
9 23716957113345 · 2⁶⁶⁶⁶⁶⁶ - 1 200700 p199 Feb 2011 term 3, difference 2697434638065 · 2⁶⁶⁶⁶⁶⁸
10 11638738675125 · 2⁶⁶⁶⁶⁶⁷ - 1 200700 p199 Mar 2011 term 3, difference 9571322415225 · 2⁶⁶⁶⁶⁶⁶
11 14646182194005 · 2⁶⁶⁶⁶⁶⁶ - 1 200700 p199 Mar 2011 term 3, difference 3388839720735 · 2⁶⁶⁶⁶⁶⁶
12 2968802755 · 2459# + 1 1057 p155 Apr 2009 term 8, difference 359463429 · 2459#
13 6179783529 · 2411# + 1 1037 p102 Jun 2003 term 8, difference 176836494 · 2411#
14 115248484057 · 2371# + 1 1014 p308 Apr 2013 term 8, difference 7327002535 · 2371#
15 113236255068 · 2371# + 1 1014 p308 Apr 2013 term 8, difference 6601354956 · 2371#
16 112929231161 · 2371# + 1 1014 p308 Apr 2013 term 8, difference 6982118533 · 2371#
17 492590931 · 2⁸⁰⁰⁰⁰ - 1631979959 · 2²⁵⁰⁰¹ - 1 24092 p199 Oct 2010 term 4, difference 164196977 · 2⁸⁰⁰⁰⁰ - 1631979959 · 2²⁵⁰⁰⁰
18 2996180304 · 7001# + 1 3019 p155 Feb 2012 term 6, difference 46793757 · 7001#
19 2946259686 · 7001# + 1 3019 p155 Feb 2012 term 6, difference 313558156 · 7001#
20 2915000572 · 7001# + 1 3019 p155 Feb 2012 term 6, difference 3093612 · 7001#

Related Pages

Jens Kruse Andersen's excellent Primes in Arithmetic Progression Records
Announcement of ten primes in arithmetic progression

References

BH77
C. Bayes and R. Hudson, "The segmented sieve of Eratosthenes and primes in arithmetic progression," Nordisk Tidskr. Informationsbehandling (BIT), 17:2 (1977) 121--127. MR 56:5405
Chowla44
S. Chowla, "There exists an infinity of 3--combinations of primes in A. P.," Proc. Lahore Phil. Soc., 6 (1944) 15--16. MR 7,243l
Corput1939
A. G. van der Corput, "Über Summen von Primzahlen und Primzahlquadraten," Math. Ann., 116 (1939) 1--50.
DN97
H. Dubner and H. Nelson, "Seven consecutive primes in arithmetic progression," Math. Comp., 66 (1997) 1743--1749. MR 98a:11122 (Abstract available)
GH79
E. Grosswald and P. Hagis, Jr., "Arithmetic progression consisting only of primes," Math. Comp., 33:148 (October 1979) 1343--1352. MR 80k:10054 (Abstract available)
Grosswald82
E. Grosswald, "Arithmetic progressions that consist only of primes," J. Number Theory, 14 (1982) 9--31. MR 83k:10081
GT2004a
B. Green and T. Tao, "The primes contain arbitrarily long arithmetic progressions," Ann. Math., preprint. Available from http://arxiv.org/abs/math/0404188v6.
GT2004b
B. Green and T. Tao, "A bound for progressions of length k in the primes," (2004) preprint.
GT2006a
B. Green and T. Tao, "Linear equations in primes," (2006) preprint. Available from http://arxiv.org/abs/math/0606088.
Guy94 (section A6)
R. K. Guy, Unsolved problems in number theory, Springer-Verlag, New York, NY, 1994. ISBN 0-387-94289-0. MR 96e:11002 [An excellent resource! Guy briefly describes many open questions, then provides numerous references. See his newer editions of this text.]
LP67
L. J. Lander and T. R. Parkin, "On first appearance of prime differences," Math. Comp., 21:99 (1967) 483-488. MR 37:6237
Rose94 (Chpt 13)
H. E. Rose, A course in number theory, second edition, Clarendon Press, New York, 1994. pp. xvi+398, ISBN 0-19-853479-5; 0-19-852376-9. MR 96g:11001 (Annotation available)

Chris K. Caldwell © 1996-2013 (all rights reserved)