How Fast are the Primes Growing?
 Introduction
Introduction
The Prime Pages keeps a list of the 5000 largest known primes, plus a few each of certain selected archivable forms and classes. These forms are defined in this collection's home page. To make the top 5000 today a prime must have 585030 digits. This is increasing at roughly 50,000 digits per year. As can be seen in the logarithmic graph below, the number of digits in the nth largest known prime is vaguely linear with time. So there is a nearly exponential growth in the rate at which the number of digits is growing each year!
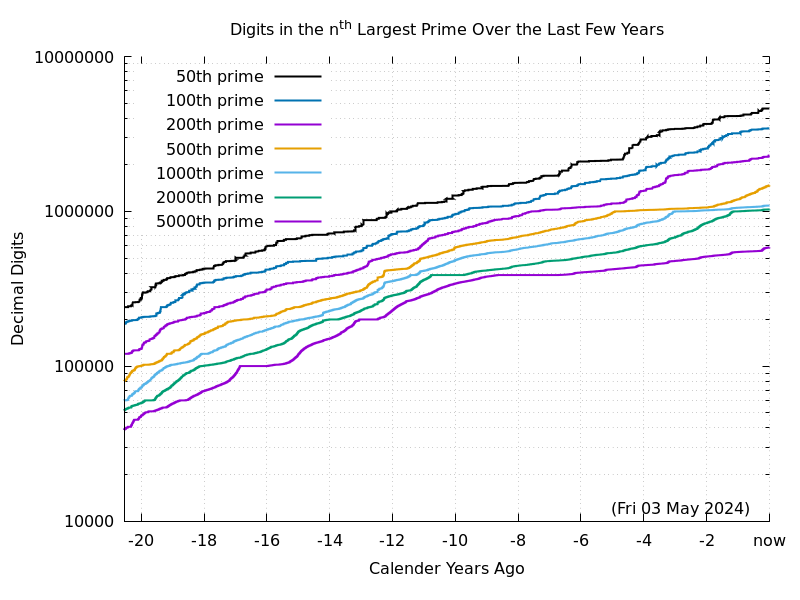
(Graphic originally by Phil Carmody.)
 A Primal Moore's Law
A Primal Moore's Law
In 1965, Gordon Moore, a co-founder of Intel, was asked to write an article predicting the development of semiconductor industry for the next decade. Moore used the data from the previous six years to predict that the number of components on the chips with the smallest manufacturing costs per component would double roughly every year. In 1975 he reduced the estimate to doubling every two years. (The current rate seems to be closer to doubling every four years.)
Later, an Intel colleague combined Moore's Law with the fact that clock speeds were increasing, to conclude that computing power is doubling every 18 months. This power form of Moore's law may be the most common in circulation today, even though it did not originate with Moore himself. Recent prognosticators have restated Moore's law in an economic form: the cost of computing power halves every x months.
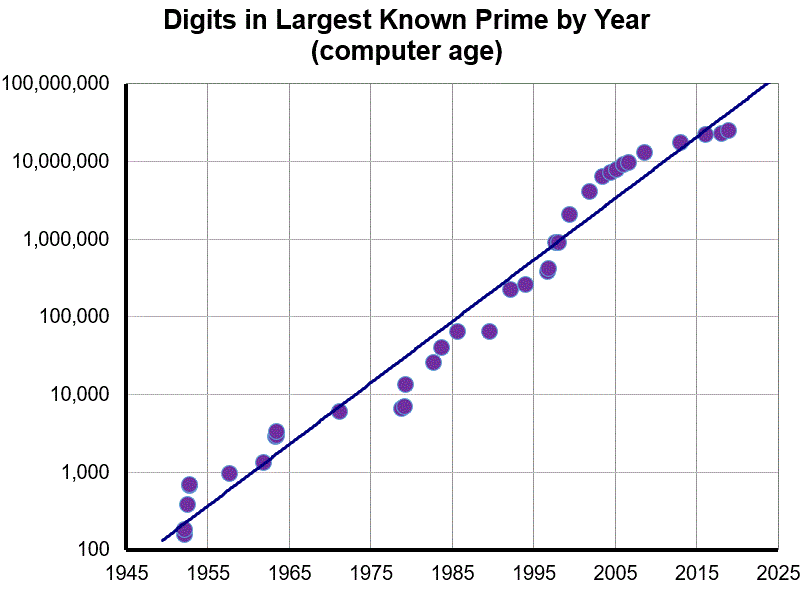
It seems reasonable (from graphs like those above and on the side) to assume a power form of Moore's law applies search for large primes:
The computing power devoted to finding large primes is is increasing exponentially.
This increase in power could come from the increased transistor density, from faster clock speeds, from cheaper component costs, or from the aggregation of computing power into organized Internet projects like GIMPS and BOINC.
As we have discussed elsewhere on this pages, the amount of time required to find a prime the same size as n is about
O((log n)3 log log n).
So if the computing power available for seeking primes doubles every k months, then the size of the largest known prime should double every 3k months. The slope 0.079 (over past 60 years) corresponds to doubling the digits every 3.8 years, or 46 months. So a quantified form of the primal Moore's law might be:
The computing power available for seeking primes doubles every 16 months.