Often we are asked a question starting "are there any primes of the
form ... ?" One of the classic ways to finish that question is "ak+l"
where k and l are fixed integers, and a takes on
the values 0, 1, 2, ... . For example, if k is 4 and l is
1, we are asking are there infinitely many primes in the following list?
1, 5, 9, 13, 17,
21, 25, 29, 33, ...
We see several already, so we might guess that there are. But what if k
is 4 and l is 2, then we are asking are there infinitely many primes
in the following list?
2, 6, 10, 14, 18, 22, 26, 30, 34, ...
Obviously not! In fact it is a trivial exercise to prove that if there is
more than one prime in the arithmetic sequence generated by k and
l:
l, l+k, l+2k, l+3k,
l+4k, ... ,
then k and l, are relatively prime (i.e., there is no positive
integer that divides both k and l except 1). But is this relatively
prime condition enough to guarentee infinitely many primes? Dirichlet answered
yes over 150 years ago by proving the following.
Dirichlet's Theorem on Primes in Arithmetic Progressions
(1837)
If k and l are relatively prime positive
integers, then the arithmetic progression
l, l+k, l+2k, l+3k,
...
contains infinitely many primes.
Often knowing that there are infinitely many primes is enough, but sometimes
we need more information--perhaps an estimate of how many are less than
or equal to n for any given n (such as the prime number theorem gives in the
case k=1). When the prime number theorem was proved, it then followed
that
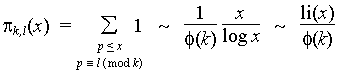
It is possible to give error estimates such as the following.
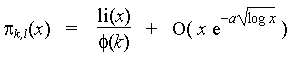
This was proved, for example, with a=1/15 [Walfisz63].
