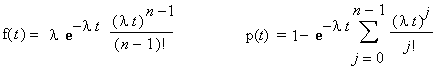FAQ: Where is the Next Mersenne Prime?
By Chris Caldwell
[ See also: Deriving the Wagstaff Mersenne Conjecture ]
Where is the next Mersenne prime? To answer this question, let Mn be the nth Mersenne prime. Take a careful look at the graph of log2(log2(Mn)) versus n. (That is, the logarithm base two of the logarithm base two of the nth Mersenne.)
 >
> One can not miss that this graph is amazingly linear. Perhaps just as amazing is that this is just what one would predict using simple heuristic arguments. In 1964 Gillies made a conjecture implying the slope is 1/2 [Gillies64]. Unfortunately his heuristic contradicts the prime number theorem. In 1980 both Lenstra and Pomerance independently conjectured there are asymptotically (egamma/log 2) log log x Mersenne primes less than x [Pomerance81]. In what follows we will address this conjecture in the tripartite form given by Wagstaff a couple years later [Wagstaff83]:
- The number of Mersenne primes less than or equal to x is about (egamma/log 2) * log log x. (Again gamma is Euler's constant).
- The expected number of Mersenne primes 2p-1 with p between x and 2x is about egamma.
- The probability that 2p-1 is prime is about (egamma log ap )/(p log 2) where a=2 if p=3 (mod 4) and a=6 if p=1 (mod 4).
This means that the geometric mean of the ratio of two successive Mersenne exponents is 2 raised to 1/egamma or about 1.47576. The fact this is close to 3/2 is probably the reason Eberhart (and many others after him) looked at his limited data and guessed that the ratio is exactly 3/2. This does appeal to those with neo-Pythagoristic tendencies (those who think numbers should be rational), but has very little other argument in favor of it.
Empirical Data from the First Mersennes
Let's compare this conjecture to our graph: if it is correct, then the distribution of the log of the log of the Mersennes is a Poisson process and if we graph log2(log2(Mn)) versus n we should get approximately a straight line with slope 1/egamma (about 0.56145948). Indeed, using the first 51 (known) Mersennes we get a regression line with slope 0.5366 and a correlation coefficient R2 = 0.9885. Not too bad.
The gaps in any Poisson process should also exhibit specific behaviors. For example, the list of the nth gaps should be uncorrelated (we get R = -0.222 for the first 50 gaps). Also their mean and standard deviation should be near the parameter for the distribution (we get 0.531 and 0.459 respectively, relatively near the parameter 1/egamma = 0.561...).
Further, the cumulative distribution of the gaps between values of a Poisson process should be governed by an exponential distribution. In particular, the probability density f(t) for the gaps and the probability p(t) the gap length is as follows [Ross93, p215].
(Usually the parameter t is a Poisson process is time, here it is log2(log2(Mn)).)
Noll's nebulous "Island Theory" for Mersennes (which I have never seen quantified) seems to roughly state that Mersennes occur in clumps with gaps between them. Perhaps so, but that is exactly what you would expect from any Poisson process!
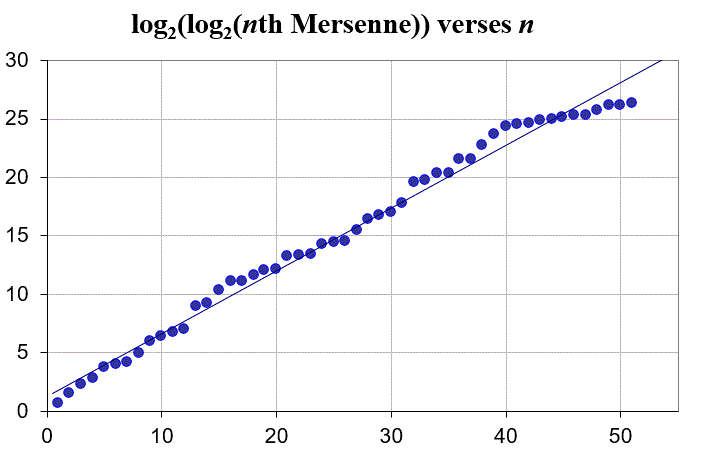
Next let's check the predicted Poisson gap distribution against the gaps between the known Mersennes. In the graph below I plot the observed cumulative frequencies of these gaps (red points) versus the expected distribution (brown curve) for the known Mersenne gaps. Again the match is excellent for the relatively few data points we have! (See [Schroeder83] for a similar analysis of the first 28 Mersennes.)
Finally, if this distribution is Poisson with mean egamma and we view log2(log2(Mn))as our 'time' scale we expect about 1.78 Mersennes per interval. Dividing the log2(log2(Mn)) scale so far explored into 27 intervals: [0,1), [1,2), ..., [26,27) and counting the number of Mersennes in each we get the following.
| Mersennes | Observed | Expected |
|---|---|---|
| 0 | 3 | 4.5 |
| 1 | 8 | 8.1 |
| 2 | 8 | 7.2 |
| 3 | 6 | 4.3 |
| 4+ | 2 | 2.9 |
A goodness-of-fit test then gives us a Chi-squared value of 1.54 and a p-value of about 0.82. This could provide weak evidence that this is a Poisson with mean egamma well. (More technically: if it were such a distribution, then the probability of seeing a Chi-squared value this much larger than 0 due to "sampling error" alone would be about 82%)
What about the next Mersenne?
So what can we gather from this? One thing is that given one Mersenne prime exponent's p, the next one will fall, on the average, near 1.47576p. But not too near the average much of the time--sometimes the gaps will be small, sometimes large. So the next larger Mersenne exponent might be over 85,000,000 yielding a Mersenne with nearly 26 million digits. Or it may not.
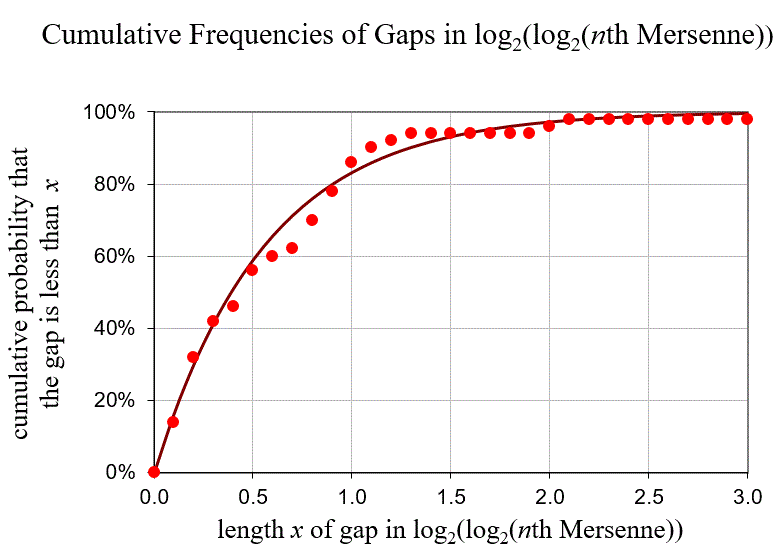
Lets be more specific graphically. If we had no idea what the first Mersennes were, we would predict values for t=log2(log2(Mn)) as follows.
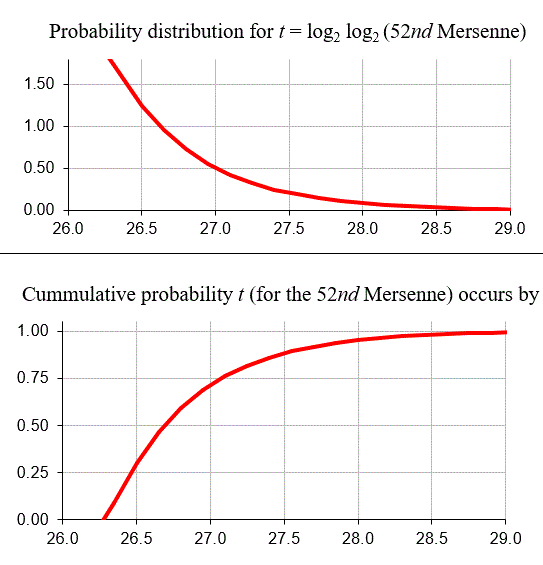
But we do know 51 Mersennes. Suppose they are the first 51 (that is, there are no primes below the 51st that lies undiscovered--remember not all of these numbers have been tested yet). So if those we know are the first 51, then we need only look at the expected gap (Poisson processes essentially "start over" after each event). Now we get the much narrower graphs:
Where do these conjectures come from?
They come from Wagstaff's article: [Wagstaff83]. But that answer is not much help is it? So we created a separate page deriving the Wagstaff Mersenne conjectures.
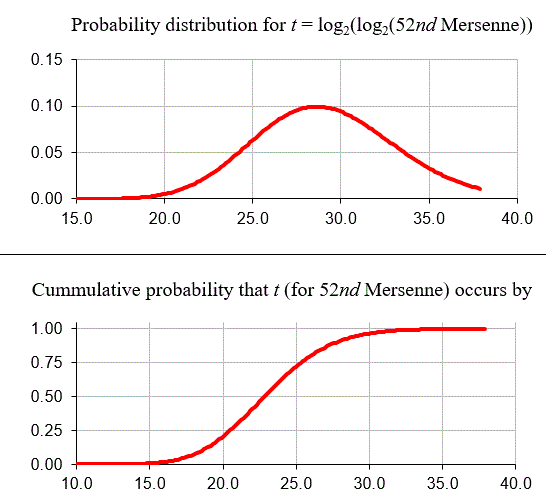
For fun let's end with two more graphs: the probability density graph for the nth Mersenne, and the probability that it occurs before a given t = log2(log2(Mn))--both assuming no knowledge of previous Mersennes.
_3d.gif)
_3d.gif)