The Top Twenty--a Prime Page Collection

Cunningham Chains (1st kind)

This page : Definition(s) | Records | Weighted Records | References | Related Pages |

The Prime Pages

Let me know if something in the Top20 is not working (caldwell@utm.edu).

The Prime Pages keeps a list of the 5000 largest known primes, plus a few each of certain selected archivable forms and classes. These forms are defined in this collection's home page. This page is about one of those forms. Comments and suggestions requested.

(up) Definitions and Notes

Recall that a Sophie Germain prime is a prime p such that q=2p+1 is also prime.  Why not also ask that r=2q+1 is prime, and 2r+1 is prime, and...? A Cunningham chain of length k of the first kind is a sequence of k primes, each which is twice the proceeding one plus one.  For example, {2, 5, 11, 23, 47} and {89, 179, 359, 719, 1439, 2879}.  This means the terms in such a sequence are p, 2p+1, 4p+3, 8p+7, ... so if a prime is labelled "(4p+3)" in the table of primes, it is the third term in a sequence of (at least) three primes.

We have a separate page about the Cunninham chains of the second kind and the Sophie Germain primes.  Cunningham chains (of both kinds) are also called chains of nearly doubled primes.

For any given length k there should be infinitely many chains of length k.  In fact the number less than N should be asymptotic to

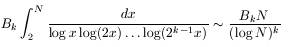
heuristic equation
where
heuristic equation
where the sequence Bk begins approximately 1.32032 (k=2), 2.85825, 5.553491, 20.2636, 71.9622, 233.878, 677.356.

Because the Sophie Germain primes have their own Top Twenty page, they are not included in the list of records below. Forthe same reason 'Cunningham Chain (p)'s and 'Cunningham Chain (2p+1)'s (which are Sophie Germain primes) are omitted.

(up) Record Primes of this Type

rankprime digitswhowhencomment
11128330746865 · 266441 - 1 20013 p158 Feb 2020 Cunningham chain (4p + 3)
21815615642825 · 244046 - 1 13272 p395 Nov 2016 Cunningham chain (4p + 3)
3778965587811 · 236627 - 1 11038 p395 Sep 2016 Cunningham chain (4p + 3)
4272879344275 · 236622 - 1 11036 p395 Aug 2016 Cunningham chain (4p + 3)
5333645655005 · 235549 - 1 10713 p364 Mar 2015 Cunningham chain (4p + 3)
6109766820328 · 7877# - 1 3385 p395 Oct 2016 Cunningham chain (8p + 7)
7231692481512 · 7517# - 1 3218 p395 Sep 2016 Cunningham chain (8p + 7)
8375967981369 · 6907# · 8 - 1 2972 p382 May 2017 Cunningham chain (8p + 7)
9354362289656 · 6907# · 8 - 1 2972 p382 May 2017 Cunningham chain (8p + 7)
10285993323512 · 6907# · 8 - 1 2972 p382 May 2017 Cunningham chain (8p + 7)
1154201838768 · 3917# - 1 1681 p395 Oct 2016 Cunningham chain (16p + 15)
1216 · 199949435137 · 3499# - 1 1494 p382 Mar 2016 Cunningham chain (16p + 15)
135780736564512 · 3023# - 1 1301 p364 Mar 2015 Cunningham chain (16p + 15)
1468002763264 · 2749# - 1 1185 p35 Mar 2012 Cunningham chain (16p + 15)
15587027392600 · 2477# · 16 - 1 1070 p382 Mar 2016 Cunningham chain (16p + 15)
1689595955370432 · 2371# - 1 1017 p364 Mar 2015 Cunningham chain (32p + 31)

(up) Weighted Record Primes of this Type

For amusement purposes only we might seek to weight the chains on the list of largest known primes by an estimate of how rare chains of that length are. We also include the Sophie Germain primes because they are chains of length two.

To form a weight we start with the usual estimate of how hard it is to prove primality of a number the size of n

log(n)2 log log n
and multiply it by the expected number of potential candidates to test before we find one of length k (by the heuristic estimate above)
log(n)k / Bk.
We then take the log one more time to make the numbers nice and small.

(Because the Sophie germain primes have their own Top Twenty page, they are not included in the list of records below.)

rankprime digitswhowhencomment
189595955370432 · 2371# - 1 1017 p364 Mar 2015 Cunningham chain (32p + 31)
254201838768 · 3917# - 1 1681 p395 Oct 2016 Cunningham chain (16p + 15)
316 · 199949435137 · 3499# - 1 1494 p382 Mar 2016 Cunningham chain (16p + 15)
45780736564512 · 3023# - 1 1301 p364 Mar 2015 Cunningham chain (16p + 15)
568002763264 · 2749# - 1 1185 p35 Mar 2012 Cunningham chain (16p + 15)
6587027392600 · 2477# · 16 - 1 1070 p382 Mar 2016 Cunningham chain (16p + 15)
7109766820328 · 7877# - 1 3385 p395 Oct 2016 Cunningham chain (8p + 7)
8231692481512 · 7517# - 1 3218 p395 Sep 2016 Cunningham chain (8p + 7)
9375967981369 · 6907# · 8 - 1 2972 p382 May 2017 Cunningham chain (8p + 7)
10354362289656 · 6907# · 8 - 1 2972 p382 May 2017 Cunningham chain (8p + 7)
11285993323512 · 6907# · 8 - 1 2972 p382 May 2017 Cunningham chain (8p + 7)
121128330746865 · 266441 - 1 20013 p158 Feb 2020 Cunningham chain (4p + 3)
131815615642825 · 244046 - 1 13272 p395 Nov 2016 Cunningham chain (4p + 3)
14778965587811 · 236627 - 1 11038 p395 Sep 2016 Cunningham chain (4p + 3)
15272879344275 · 236622 - 1 11036 p395 Aug 2016 Cunningham chain (4p + 3)
16333645655005 · 235549 - 1 10713 p364 Mar 2015 Cunningham chain (4p + 3)

(up) Related Pages

(up) References

Cunningham1907
A. Cunnningham, "On hyper-even numbers and on Fermat's numbers," Proc. Lond. Math. Soc., series 2, 5 (1907) 237--274.
Guy94 (SectionA7)
R. K. Guy, Unsolved problems in number theory, Springer-Verlag, New York, NY, 1994.  ISBN 0-387-94289-0. MR 96e:11002 [An excellent resource! Guy briefly describes many open questions, then provides numerous references. See his newer editions of this text.]
Lehmer1965
D. H. Lehmer, "On certain chains of primes," Proc. Lond. Math. Soc., series 3, 14a (1965) 183--186.  MR 31:2222
LM1980
C. Lalout and J. Meeus, "Nearly-doubled primes," J. Recreational Math., 13 (1980-81) 30--35.
Loh89
G. Löh, "Long chains of nearly doubled primes," Math. Comp., 53 (1989) 751-759.  MR 90e:11015 (Abstract available) [Chains of primes for which each is either twice the proceeding one plus one, or each is either twice the proceeding one minus one. See also [Guy94, section A7].]
Ribenboim95 (p 333)
P. Ribenboim, The new book of prime number records, 3rd edition, Springer-Verlag, New York, NY, 1995.  pp. xxiv+541, ISBN 0-387-94457-5. MR 96k:11112 [An excellent resource for those with some college mathematics. Basically a Guinness Book of World Records for primes with much of the relevant mathematics. The extensive bibliography is seventy-five pages.]
Yates82
S. Yates, Repunits and repetends, Star Publishing Co., Inc., Boynton Beach, Florida, 1982.  pp. vi+215, MR 83k:10014
Chris K. Caldwell © 1996-2021 (all rights reserved)